Appunti di Meccanica Celeste

Aggiornamento del 21/10/2022
III ediz. del 30/08/2006
II ediz. del 17/08/2002
I ediz. del 30/12/1988

Autore: Giuseppe Ferruzzi – IKØDWJ

Premessa dell’Autore

I numerosi appunti sugli elementi di meccanica celeste, scritti durante il mio percorso di interesse iniziale all’operatività via OSCAR10, hanno dato origine a questo compendio che ho cercato di assemblare in modo logico e coerente. Per me è stato un insegnamento preparatorio che mi ha permesso di intraprendere l’affascinante attività radioamatoriale via satellite. L’intenzione, anche se non effettivamente realizzata, era di capire come venissero manipolati i parametri necessari per ottenere, istante per istante, il preciso puntamento delle antenne verso un satellite artificiale orbitante.
Queste nozioni mi dettero un ulteriore impulso nel diletto dello studio dell’astronomia e a osservare il cielo visibile di notte come astrofilo. Invece di azionare i rotori delle antenne per l’inseguimento di un micro-satellite artificiale orbitante, avrei dovuto azionare gli attuatori di un telescopio motorizzato su un oggetto celeste naturale, molto più grande, nella profondità dello spazio cosmico.

Indice generale:

Parte 1ª – Cenni sul sistema di coordinate astronomiche

Introduzione
Sfera celeste
Ascensione Retta
Declinazione
Declinazione solare ed Eclittica
Primo punto di Ariete
Eclittica polare
Meridiano
Giorno solare medio
Anno tropico
Calendario Giuliano
Calendario Gregoriano
Fascia tropicale
Tempo Sidereo

Parte 2ª – Satelliti artificiali

La dinamica orbitale
Orbite tipiche dei satelliti artificiali
Inclinazione orbitale, nodo ascendente e discendente
Ascensione retta del nodo ascendente
Moto medio e periodo orbitale
Epoca di riferimento
Argomento del perigeo
Eccentricità orbitale
Anomalia media, vera ed eccentrica
La Phase
Effetto giroscopico e l’asse Z del satellite
Angolo di strabismo dell’asse Z
Effetto Doppler
Attenuazione di tratta

Introduzione

I radioamatori sono stati i precursori nell’utilizzo casalingo dei computers, il merito lo si è dovuto alle prospettive d’uso all’interno di una stazione operativa.
La possibilità concreta del controllo centralizzato automatico e interattivo delle varie apparecchiature radio e degli attuatori delle antenne permise l’accesso a opportunità operative che tradizionalmente erano ottenibili solo con sistemi elettronici progettati appositamente, più complessi e costosi, la cui specificità li rendeva vincolati nel proprio campo d’utilizzo.
Delegare ogni singolarità al computer per mezzo di software adeguati significava invece flessibilità, riduzione dei costi dell’elettronica a piccole interfacce, efficienza operativa e alleggerimento del lavoro svolto dall’operatore. Questi risultati stimolavano nuove aspettative d’applicazione che sempre più numerose e diversificate implicavano ogni campo d’interesse.
Tuttavia non si può operare senza avere almeno le conoscenze essenziali. Il tracking dei satelliti con le sue problematiche funzionali rendeva necessaria una conoscenza minima di astronomia e questi appunti sono il frutto di conoscenze acquisite dal sottoscritto durante quel periodo.
Prendiamo ora per esempio una navetta spaziale, una volta messa in orbita è soggetta alle stesse leggi fisiche che regolano gli altri corpi celesti naturali. Per ragioni di costi, di studio e sperimentazione, i satelliti artificiali per uso radioamatoriale non venivano previsti per essere lanciati in orbite di tipo geostazionario ma, di tipo orbitante. Fra queste tipologie, quelle ellittiche erano le più adatte. Ogni satellite ha un “punto di visione” che coincide col centro della navetta spaziale sul cui asse di rotazione viene orientato il lobo d’irradiazione principale delle antenne direttive di bordo. L’angolo di apertura è misurato a -3dB dal suo punto di massimo guadagno ed è quello che poi determina sulla superficie terrestre un’impronta utile, ossia una “zona d’illuminazione” in cui si possono misurare gradienti di energia elettromagnetica in dBm. Periodicamente varie parti della superficie terrestre ne sono interessate, la loro estensione permette collegamenti radio via satellite anche tra radioamatori di continenti diversi.
Le emissioni radioelettriche di questi setelliti sono a polarizzazione circolare e per quanto riguarda il sistema d’antenna utilizzato a terra dai radioamatori la scelta si concentra su forme strutturali di tipo elicoidale o di tipo yagi a dipoli incrociati configurati per una polarizzazione circolare sinistrorsa o destrorsa ^[1].
Le frequenze di uplink e downlink utilizzano le bande VHF-UHF ed SHF, il motivo è duplice, sia perché sono frequenze che superano abbondantemente la massima frequenza usabile (MUF) per la riflessione da parte della ionosfera sia per il fatto di poter disporre sulle limitate dimensioni della navetta spaziale di antenne di elevato guadagno ma di piccoli ingombri. Ogni satellite orbitante ha una vita teorica definita, determinata nella sostanza dalla tenuta delle batterie di bordo che entrano in funzione nei tratti d’orbita quando i pannelli solari della navetta spaziale non sono illuminati dal sole, un altro fattore importante della vita di un satellite artificiale è il decadimento molto lento ma progressivo della sua orbita che lo fa avvicinare sempre più alla terra. Quest’ultimo parametro insieme ai sette numeri per definirne l’orbita, di cui se ne da nozione più avanti, costituiscono i parametri fondamentali degli “elementi kepleriani” presenti nei dati TLE, acronimo di Two Line Elements o formato a due linee, disponibili al seguente indirizzo URL:
https://www.amsat.org/tle/current/.
Il file di testo da scaricare è il “daily.all” che va utilizzato come file locale per aggiornare i dati TLE sul proprio programma di monitoraggio.

Gli otto elementi fondamentali per definire l’orbita di un satellite sono:

Epoca di riferimento Tø;
Inclinazione orbitale Iø;
Ascensione retta del nodo ascendente Oø;
Argomento del perigeo Wø;
Eccentricità Eø;
Moto medio Nø;
Anomalia media Mø;
Decadimento N1.

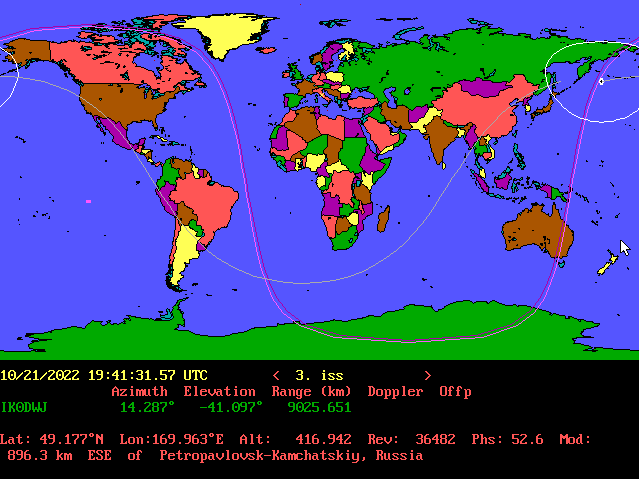
Negli anni Ottanta MS-DOS (Microsoft Disk Operating System) era il sistema operativo che usavo sul mio PC, pertanto nel periodo di funzionamento del satellite Oscar10 utilizzavo il programma InstantTrack di cui ne ammiravo la grafica, mi piaceva molto, era unica. Tuttora lo considero il miglior programma per l’inseguimento istantaneo dei satelliti orbitanti e sebbene lo posso avviare solo tramite l’emulatore “Dosbox”, riprovo sempre le stesse sensazioni di allora.

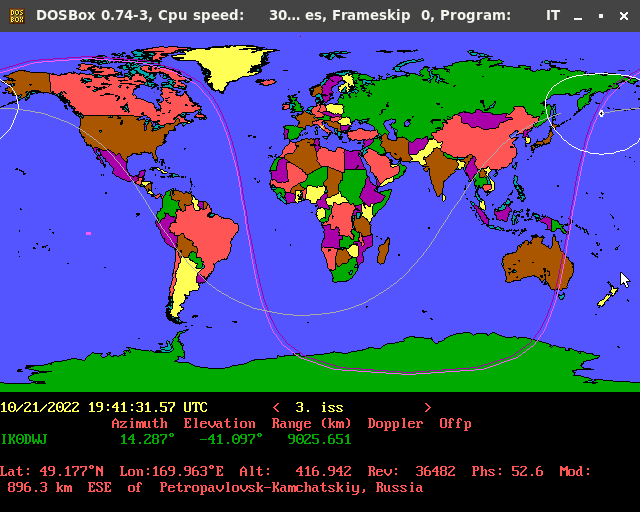
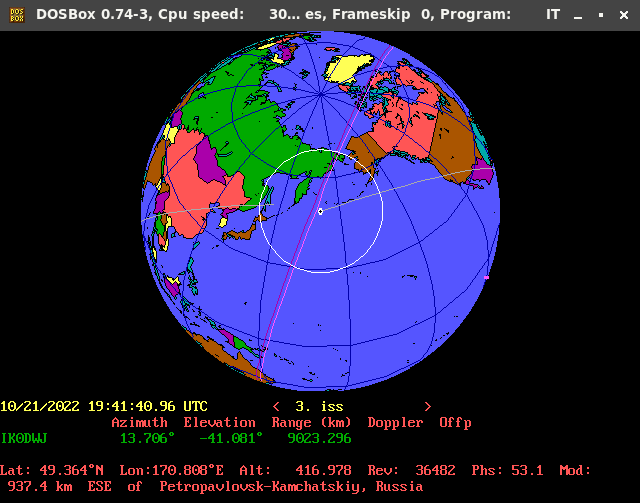
L’ultima versione 1.5 stabile di InstantTrack funziona perfettamente e può essere scaricata al seguente indirizzo URL:
https://www.mustbeart.com/software/it/getit.html.

^[1] L’esatta scelta del tipo di polarizzazione da utilizzare durante il tracking in certe particolari situazioni è importante e può determinare attenuazioni notevoli e compromettere l’efficienza del proprio sistema d’antenna.
Per esempio, se lungo una path non riflettente, l’antenna del satellite e l’antenna terrestre fossero allineate otticamente ma con polarizzazione circolare contraria, non si riceverebbe nessun segnale perché l’attenuazione reciproca sarebbe teoricamente infinita; se invece l’antenna terrestre avesse avuto una polarizzazione lineare (verticale oppure orizzontale), l’attenuazione sarebbe risultata di soli -3dB. Tuttavia i decibel sono pesanti e anche i -3dB di attenuazione derivati dalla formula N=10·log₍₁₀₎P2/P1 significano che la sua attenuazione in potenza vale 2, ossia 10^(3/10), infatti 3dB=10·log₍₁₀₎2; in questa situazione sebbene l’antenna terrestre in fase di ricezione sottrarrebbe la metà della potenza, il segnale del satellite può essere ricevuto e viceversa.
Questo spiega il perché, quando si usano antenne a polarizzazione circolare, è molto importante poter invertire il senso di rotazione elettrica nei dipoli incrociati della propria antenna.

Sistema di coordinate astronomiche

“Sfera celeste”

Nel nostro sistema di riferimento la sfera celeste si deve intendere idealmente una sfera trasparente di dimensione arbitraria. Questa sfera immaginaria viene posta in modo tale che la Terra ne risulti all’interno e al centro assumendone il modello originale in miniatura e proiettandone su questa superficie ideale le coordinate del sistema equatoriale terrestre ossia il reticolo costituito dall’equatore con i suoi paralleli e meridiani, così si ha un equatore celeste che divide anche il cielo della sfera celeste in emisfero boreale e australe mentre i paralleli e meridiani ora prendono rispettivamente il nome di Declinazione (Dec.) e Ascensione Retta (A.R.); l’unica differenza è che l’ascensione retta può indifferentemente essere espressa sia in misura angolare: gradi (°), primi (‘) e secondi (“); sia in tempo: ore (h), minuti (m), secondi (s). Tuttavia è più in uso questo secondo metodo, perché l’Ascensione Retta è anche riferita direttamente al tempo siderale o ora stellare. Vedere (fig. 1)

“Ascensione Retta” [A.R.]

Il meridiano corrispondente a 0 ore, o equivalentemente a 24 ore, sulla Terra è il meridiano di Greenwich, mentre sulla sfera celeste passa per il Primo punto d’Ariete, o equinozio di primavera. L’ascensione retta è misurata sull’equatore celeste da questo punto in direzione est fino al valore di 24 ore, corrispondente ad un angolo giro (360°).

“Declinazione” [Dec.]

Si misura in gradi dall’equatore celeste, posto a 0°, positivamente verso nord e negativamente verso sud, sino a raggiungere i due poli celesti posti a +90°(nord) dell’emisfero boreale e -90° (sud) dell’emisfero australe.

“Declinazione solare ed Eclittica”

La risultante di tutte le declinazioni del sole rispetto all’equatore che un osservatore terrestre potrebbe misurare giorno per giorno quando il sole gli passa al meridiano locale a mezzogiorno è all’origine dell’Eclittica che in definitiva è la proiezione sulla sfera celeste dell’orbita della Terra attorno al sole.
L’eclittica varia rispettivamente da 0° equinozio di primavera (il 21 marzo) a +23°,44 detto solstizio di estate (il 21 giugno), per passare poi ancora a 0° equinozio d’autunno (il 23 settembre), per arrivare infine ad una declinazione corrispondente a – 23°,44 detto solstizio d’inverno (il 21 dicembre ); poi si ripete il ciclo. Agli equinozi vedremo il sole tracciare dall’alba al tramonto la linea ideale dell’equatore celeste; chi si trova all’equatore vedrà tracciare un arco passante proprio allo zenit sopra la sua testa (lo zenit è il punto della sfera celeste situato sulla verticale rispetto all’osservatore).
Come si deduce dalla (fig. 1), il cambiamento delle stagioni dipende dalla posizione della declinazione solare: quando la massima declinazione solare avviene nei paesi situati sopra l’equatore terrestre, ossia nell’emisfero boreale, vi è la stagione più calda; mentre è invece la stagione più fredda nell’altro emisfero della Terra, quello australe.

“Primo punto di Ariete”

La retta che sale dal centro della Terra, e che attraversa idealmente il Sole giacente sul piano equatoriale celeste all’equinozio di primavera o punto vernale, ai tempi di Tolomeo cadeva nella costellazione dell’Ariete, per questo prese il nome di “Primo punto d’Ariete” o punto γ (gamma). Il lento cambiamento della direzione nello spazio dell’asse di rotazione terrestre, vedi Eclittica polare, a causa dell’influenza gravitazionale della Luna, del Sole e dei pianeti del sistema solare, determina una precessione degli equinozi, consistente nel fatto che il Sole ritorna ogni anno al punto vernale prima di avere compiuto nel suo moto apparente l’intero percorso dell’eclittica, pertanto il punto γ non ha una direzione spaziale statica ma descrive nel tempo di 26.000 anni tutti i punti dell’eclittica attraversando le 12 costellazioni dello zodiaco, vedere le (fig. 2 e 3). Attualmente il punto γ è situato alla fine della costellazione dei Pesci.

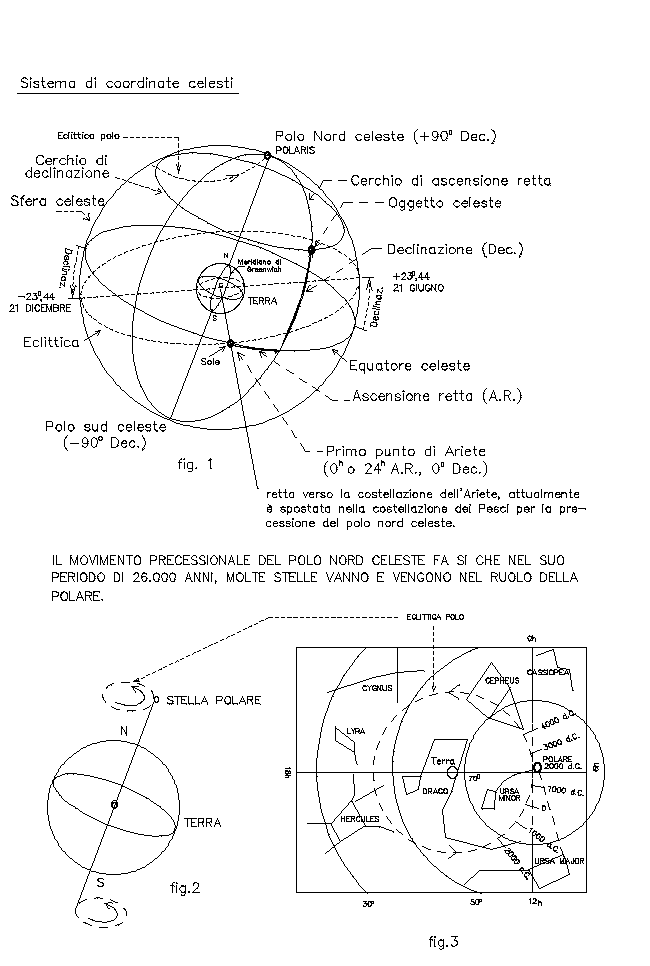
Fig. 1,2,3 – Sistema di coordinate celesti e la precessione del polo nord celeste.

“Eclittica polare”

Immaginiamo all’oscillazione del perno di una trottola che gira, mentre per quest’ultima un’oscillazione completa avviene in frazioni di secondo per l’asse terrestre questa oscillazione viene completata in circa 26.000 anni, quindi le coordinate celesti quelle usate in astronomia, variano al massimo di circa 1/70 di grado ogni anno. La stella polare (Polaris dell’Ursa minor) quindi non potrà essere sempre la stella del polo nord, lo potrà essere solo ciclicamente, ora lo è per il nostro millennio il 2000 d.C.
Il cerchio descritto da questo moto precessionale del polo nord è molto esteso; con l’attuale riferimento delle coordinate celesti esso arriva fino a circa 45° di declinazione sulla sfera celeste, occupa approssimativamente 1/16 dell’emisfero boreale celeste e lo stesso avviene in quello australe.

“Meridiano”

Il meridiano è quella metà di un cerchio massimo della sfera celeste che termina ai poli nord e sud. Sulla Terra il meridiano è una linea di longitudine. Sulla sfera celeste il meridiano che passa attraverso lo zenit è chiamato meridiano dell’osservatore.

“Giorno solare medio”

Poiché i giorni solari reali sono di durata variabile nel corso dell’anno solare (vi sono inoltre piccole fluttuazioni casuali del periodo di rotazione della Terra le cui cause non sono ancora ben chiare), si è idealmente creato un giorno convenzionale detto del Sole medio, che esprime l’intervallo fra due passaggi successivi attraverso il meridiano dell’osservatore di un corpo ideale chiamato appunto Sole medio che si muove, nel suo moto apparente, con velocità uniforme lungo l’equatore. Se il giorno solare medio è riferito al meridiano dell’osservatore posto a Greenwich ossia a 0° di longitudine esso diventa il tempo di riferimento universale chiamato GMT (tempo medio di Greenwich) oppure UT (tempo universale).

“Anno Tropico”

Mentre c’è sempre un numero intero di giorni in un anno civile, la Terra impiega effettivamente 365,2422 giorni solari medi per percorrere l’intera orbita intorno al Sole; questo è l’anno tropico, l’intervallo di tempo tra due consecutivi passaggi del Sole all’equinozio di primavera, su cui è regolato il calendario civile; usa pertanto come riferimento il primo punto di Ariete. Quando alla parola anno non viene associato un aggettivo che lo qualifichi, si intende usualmente dell’anno tropico.

“Calendario Giuliano”

Se non si tenesse conto di questo fatto e si adottasse 365 giorni per ciascun anno, allora la Terra progressivamente perderebbe il passo con il nostro sistema di riferimento al ritmo di 0,2422 giorni ogni anno. Dopo cento anni la differenza sarebbe di 24 giorni in meno; dopo 1500 anni le stagioni verrebbero invertite. Giulio Cesare cercò di mettere ordine creando per convenzione l’anno bisestile di 366 giorni, il giorno extra viene aggiunto a febbraio ogni volta che il numero dell’anno è divisibile per 4. Pertanto in un secolo, ogni 4 anni troviamo l’anno bisestile, quindi in cento anni vi sono 100/4=25 giorni in più e con questa correzione il suo anno civile medio diventa di 365 + (25/100= 0,25) ossia 365,25 giorni molto prossimo all’anno tropico di riferimento, comportando un errore medio in eccesso di (0,25-0,2422) · 100=0,78 giorni ogni cento anni.
A volte si preferisce esprimere il tempo nelle osservazioni astronomiche in giorni e decimali, con epoca fondamentale di riferimento dal mezzogiorno del meridiano di Greenwich del primo gennaio del 4713 a. C.; il numero dei giorni solari medi trascorsi da quel tempo è chiamato numero del giorno giuliano o data giuliana (JD). Ogni nuovo giorno giuliano comincia alle ore 12,00 GMT (UT), con una sfasatura di mezza giornata rispetto al giorno civile.

“Calendario Gregoriano”

Il Calendario Giuliano funzionò bene per molti secoli, fino a quando verso il 1582 si ebbe nuovamente un’apprezzabile differenza fra le stagioni e le date. Papa Gregorio migliorò allora il sistema abolendo i giorni dal 5 al 14 ottobre 1582 incluso, così che gli anni civile e tropico tornassero in riga e aggiunse una nuova regola al calendario giuliano ossia che gli anni il cui numero termina con 2 zeri (per es. 2000, 2100, ecc.) sono bisestili solo se a loro volta sono divisibili per 400. Questo sistema perde 3 giorni rispetto a quello giuliano ogni 400 anni. Secondo questo calendario 400 anni civili contengono (400 · 365)+[(0,25 · 400)-3]= 146097 giorni, cosicché la lunghezza media dell’anno civile è di 146097/400= 365,2425 giorni, una eccellente approssimazione quindi della lunghezza dell’anno tropico.

“Fascia tropicale”

Il Tropico è il parallelo sulla Terra individuato dal subpoint del Sole con la declinazione del giorno del solstizio (il subpoint è il punto sulla superficie della Terra individuato dalle coordinate geografiche, determinato dalla retta immaginaria passante per il Sole, o più in generale per un oggetto celeste, e il centro della Terra). Dalla fig.4 si può vedere graficamente la presenza di due solstizi: quello estivo detto Tropico del Cancro^[2] e quello invernale detto Tropico del Capricorno^[2], situati rispettivamente a 23° e 27′ di latitudine a nord (+) e a sud (-) dell’equatore, delineando la cosiddetta fascia tropicale.

Fig. 4 – Fascia Tropicale.

^[2] Per effetto della precessione degli equinozi, la linea congiungente i due solstizi d’estate e d’inverno si è spostata di circa 30° o 2^h sideree indietro (vedi Tempo Sidereo), e a differenza delle costellazioni sopraddette (riferite a oltre due millenni addietro), i tropici estivi e invernali cadono ora rispettivamente nelle contigue costellazioni dei Gemelli (al 21giugno) e del Sagittario (al 21 dicembre).

“Tempo Sidereo” [TS]

Come si vede dalla fig.5, costituisce l’angolo orario dell’equinozio di primavera misurato sull’equatore celeste in senso antiorario fra il meridiano di Greenwich (in questo caso diventa tempo sidereo di Greenwich) e il primo punto di Ariete corrispondente a 0^h oppure 24^h o angolo di 0° oppure di 360°. Il passaggio da gradi in ore si fa sapendo che 360°=24^h (ogni 15°=1^h). Il giorno sidereo, essendo regolato sulle stelle, anticipa di 4 minuti il giorno solare durante il quale la Terra si muove lungo la sua orbita attorno il Sole di circa un grado, spostando il meridiano di riferimento; ogni stella, quindi, dopo un giorno solare non si ripresenta più nella stessa esatta posizione precedente, ma con uno spostamento angolare in A.R. di circa 1° verso ovest. Viceversa, se ad ogni giorno sidereo ogni stella si ripresenta esattamente nella stessa posizione, il Sole sembra invece spostarsi progressivamente rispetto al primo punto di Ariete verso est. Appare evidente il motivo per cui la cadenza dei due tempi non può coincidere ^[3].

Fig. 5 – Orologio Sidereo

^[3] Esempio di conversione del tempo universale UT o GMT in tempo sidereo TS (precisione migliore di 1/10 di secondo):

Costanti di calcolo:
a=0,0657098;
b (rif. anno 1996)=17,403263;
b (rif. anno 1997)=17,353468;
b (rif. anno 1998)=17,369382;
b (rif. anno 1999)=17,385297;
b (rif. anno 2000)=17,401211;
c=1,002738;
d=0,997270.
Nota: la costante b dipende dall’anno.

Quale sarà il TS riferito a Greenwich alle ore 21 UT del 22 settembre 1996 ?

Procedimento di calcolo:
I giorni dell’anno corrispondenti fino al 22 settembre compreso sono: giorni=266
T₀=266 · a = 266 · 0,0657098= 17,478807- b= 17,478807-17,403263= 0,075544
UT · c = 21 · 1,002738= 21,057498
TS=(UT · c)+T₀=21,057498+0,075544=21,133042 ore e decimali
Se il risultato è maggiore di 24, sottrarre 24. Se il risultato è negativo, aggiungere 24.
TS= 21^h 7′
Il TS riferito a Greenwich solo all’equinozio d’autunno è coincidente con il tempo UT;
al solstizio d’inverno TS ritarda di 6 ^h rispetto a UT;
all’equinozio di primavera TS ritarda di 12^h rispetto a UT;
al solstizio d’estate TS ritarda di 7^h rispetto a UT.

Satelliti artificiali

“La dinamica orbitale”

La curvatura del nostro pianeta è tale che percorrendo idealmente una retta che parte da un punto tangenziale con il terreno, dopo 8 km di percorso orizzontale, si vede il suolo discendere di 5 metri. Supponiamo ora un cannone posto a 5 metri di altezza sulla verticale del punto tangenziale della retta suddetta e che nella direzione parallela ad essa possa sparare un proiettile ad una velocità tale (28.800 km/h) da perdere solo questi critici 5 metri di altezza ogni 8 km percorsi; ciò equivale a dire che il proiettile cadrà con la stessa velocità con cui la superficie della Terra “sfugge” sotto di lui. Risulterà così che al raggiungimento dell’ottavo chilometro, sebbene abbia perduto 5 m di quota, il proiettile si ritroverà esattamente alla stessa distanza dal suolo che aveva al momento dello sparo. Se si escludesse la forza esterna relativa alla frizione con l’aria, il proiettile persevererebbe per inerzia nel suo stato di moto e con la conservazione della velocità iniziale la situazione diventerebbe interessante: il suolo “sfuggirà” sempre davanti al proiettile e questo non riuscirà mai a cadere, entrerebbe nell’ipotesi suddetta in orbita intorno alla Terra a soli 5 metri di altezza.
Da ciò si estrae l’idea che la componente orizzontale della velocità di un satellite è un fattore determinante, ma l’influenza dell’atmosfera terrestre come forza esterna lo è ancora di più; è chiaro comunque che a quella velocità, qualsiasi veicolo verrebbe disintegrato dall’attrito con l’aria. Si rende necessario allora conoscere a quale quota l’atmosfera terrestre non potrà più contrastare in modo significativo lo stato di moto inerziale previsto per un satellite nella fase di messa in orbita.

Per maggiore chiarezza si fa qualche passo indietro e si premette la legge della gravitazione universale formulata da Newton nel XVII secolo che stabilisce che due corpi si attirano reciprocamente in ragione diretta del prodotto delle loro masse ed in ragione inversa del quadrato della loro distanza, ne deriva che la velocità che si deve imprimere ad un veicolo affinché si mantenga in orbita è in funzione dell’altezza di volo ^[4]; più l’altezza aumenta, inferiore è la velocità di mantenimento in orbita e questo indipendentemente dal peso del veicolo e, oltre una certa quota, anche dalla sua forma.

^[4] Formula per calcolare la velocità che deve avere un satellite per mantenersi in orbita ad una altezza h al di sopra della superficie terrestre:

dove R ed M sono rispettivamente il raggio e la massa della Terra, K è la costante di gravitazione universale ed h è l’altezza del satellite dalla superficie terrestre.

“Orbite tipiche dei satelliti artificiali”

Ad una quota di 400 km di altezza, l’alta atmosfera, potrebbe essere definita come spazio esterno condensato, tuttavia anch’esso disturba sufficientemente il moto inerziale di un satellite orbitante a quella quota, avviandolo in un progressivo processo di decadimento del periodo orbitale [Decay, N1]. Tutto il ciclo completo di questo lento avvicinamento a spirale del satellite alla Terra, può durare diversi anni con un orbita di 500 km di altezza, mentre a 1000 km può durare addirittura per secoli.

Il satellite descriverà un’orbita circolare se al momento di entrare in orbita terrestre la componente orizzontale della velocità del veicolo corrisponde alla velocità minima richiesta per il mantenimento in orbita; viceversa, tanto maggiore è la velocità su quella minima richiesta per una determinata quota, più l’orbita risulterà proporzionalmente allungata, fino a raggiungere il caso limite in cui si convertirà in una parabola di fuga. Le orbite dei satelliti artificiali possono essere del tipo asincrono (fig. 6a,b); questi hanno generalmente un periodo orbitale che può essere alcune volte più corto di un giorno solare. Il fascio di radiazione dell’antenna di un satellite determina sulla Terra un limite geografico di ricezione dell’energia irradiata, detta zona di illuminazione che con i satelliti asincroni cambia regolarmente le coordinate geografiche, è quindi in continuo spostamento sulla superficie terrestre. Se si volesse invece che questo limite geografico resti fisso, oppure variabile in latitudine ma fisso sullo stesso meridiano, si devono scegliere satelliti previsti per orbite sincrone ^[5], (vedi fig. 6c). Vi sono anche traiettorie speciali denominate sincrone con il Sole, con orbita a grande inclinazione il cui piano ha una precessione tale da non rientrare mai nel cono d’ombra della Terra.
In ogni caso nel punto centrale della suddetta zona di illuminazione, si ha la massima concentrazione dell’energia irradiata dalle antenne del satellite. La progressiva perdita della potenza ricevuta, espressa in dB, diviene evidente mano a mano che ci si allontana da questo centro di illuminazione a causa del graduale disallineamento, offpointing angle, tra le antenne del satellite e quelle terrestri. Per i satelliti geostazionari, dato che la zona di illuminazione è fissa, si possono determinare le cosiddette mappe di copertura del satellite dove viene rilevata questa perdita di potenza in dB.

Fig. 6 a/b/c – Orbite tipiche dei satelliti artificiali.

es:
Un satellite per una quota di volo di 10.000 km deve avere una velocità v=4,9km/s o 17.640 km/h.

^[5] Se il satellite viene predisposto per un’orbita circolare ad una distanza dalla Terra di 36.800 km d’altezza sulla verticale del piano equatoriale celeste, (vedere fig. 6c), la velocità di mantenimento in orbita coincide con la velocità di rotazione terrestre. Nel caso del satellite geostazionario, esso risulta fermo rispetto ad un punto della Terra e la posizione orbitale viene espressa in gradi longitudinali rispetto al meridiano di Greenwich.
Una variante è il satellite sincrono che alle stesse condizioni sopraddette, tranne i diversi gradi di inclinazione del suo piano orbitale su quello equatoriale terrestre, mantiene costante la sua longitudine geografica (meridiano), sebbene vari in latitudine nel percorrere la sua traiettoria orbitale.

“Inclinazione orbitale [Iø], nodo ascendente e discendente”

L’inclinazione è l’angolo formato dal piano orbitale sul piano equatoriale. Si definisce invece nodo ascendente il punto di attraversamento, da parte del satellite, del piano equatoriale in direzione nord, e nodo discendente quello in direzione sud. Il subpoint del satellite al nodo ascendente, situato sull’equatore terrestre ed individuato dalla longitudine viene denominato Aequatorcrossing [EQX], (vedi fig.7).

Fig. 7 – Inclinazione orbitale, nodo ascendente e discendente.

“Ascensione retta del nodo ascendente” [RAAN, 0ø]

Determina la distanza angolare, in senso antiorario sull’equatore celeste, dal punto primo d’Ariete alla proiezione sull’equatore celeste del nodo ascendente ( vedi fig. 8 ).

Per esempio l’ascensione retta del nodo ascendente del satellite AO10 (agli inizi della sua sfortunata attività), si spostava, in senso orario sull’equatore celeste e verso il punto primo di Ariete, di 0,137 gradi al giorno per effetto della regressione longitudinale in gradi del nodo ascendente verso ovest detta Decalage.

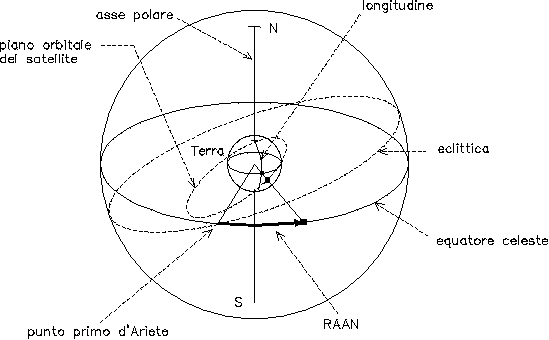
Fig. 8 – Ascensione retta del nodo ascendente.

“Il Moto medio [Nø] e il Periodo orbitale”

Il satellite in orbita circolare viaggia con una velocità costante; mentre in un’orbita non circolare (eccentricità > ø) si muove con una velocità progressivamente maggiore quando percorre, dall’apogeo al perigeo, il tragitto orbitale di avvicinamento alla Terra e progressivamente minore quando percorre, dal perigeo all’apogeo, il tragitto di allontanamento da essa. Per il calcolo del tempo impiegato in una rivoluzione attorno alla Terra, si considera la velocità media del satellite che marca uniformemente il tempo in un’orbita circolare. Questo moto convenzionale in astronomia prende il nome di moto medio la cui unità di misura è il numero delle rivoluzioni per giorno. Si definisce a sua volta una rivoluzione (rev.) o periodo orbitale il tempo determinato da due consecutivi passaggi del satellite al perigeo. Qualche volta il periodo orbitale viene usato come un elemento orbitale al posto del moto medio. Il periodo orbitale è semplicemente l’inverso del moto medio. Un satellite che ha un moto medio di 2 rivoluzioni per giorno, per esempio, ha un periodo di 12 ore. Qualche volta è invece il semiasse maggiore ad essere specificato al posto del moto medio. Tipicamente i satelliti hanno un moto medio compreso da 1 rev. per giorno a 16 rev. per giorno.

Esempi di calcolo

Cioè lo SHUTTLE viaggia alla velocità di 7,73 Km/sec (27.828 Km/h) e impiega 1,5 ore a compiere un’orbita completa. In un giorno quindi compie circa 16 orbite.

“Epoca di riferimento” [Tø]

Determina il tempo espresso in giorni e frazioni di giorno solare a partire dalle ore 00:00 UT del primo giorno dell’anno fino all’istante in cui il satellite viene considerato in un punto di riferimento preciso sull’orbita. Per esempio, AO10 all’inizio dell’orbita n. 1639 aveva una Tø di 85230.19430632 che viene interpretata in questo modo: le prime due cifre indicano l’anno di riferimento (’85), mentre 230 è il duecentotrentesimo giorno di questo anno, ossia il 18 agosto. I decimali dell’epoca di riferimento, il numero 0.19430632, rappresenta la frazione del giorno, che moltiplicato per 24 da le ore, ossia (04).6633512; i decimali del numero delle ore rappresentano le frazioni delle ore, per cui moltiplicando questi decimali per 60 da i minuti, ossia (39).801072; i decimali del numero dei minuti rappresentano le frazioni dei minuti, per cui moltiplicando questi decimali per 60 da i secondi, ossia (48).06432 decimali… Concludendo risulta il 18 agosto 04:39:48 UT.

“Argomento del perigeo” [argp, Wø]

Determina l’angolo sul piano orbitale misurato fra il nodo ascendente e il perigeo nel senso del moto del satellite e per convenzione è un angolo compreso tra 0° e 360° (vedi fig. 9). Nel satellite AO10 argp aumenta di 0,249 gradi al giorno spostando la linea degli apsidi nel verso del moto del satellite.

Fig. 9 – Argomento del perigeo.

“Eccentricità” [e, Eø]

Specifica di quanto un’orbita differisce da una perfettamente circolare. L’eccentricità ha un valore compreso tra zero e uno. Quando e=ø la ellisse è un cerchio, quando è prossima a 1 invece è molto allungata e appiattita.

“Anomalia media [ma, Mø], anomalia vera [v], anomalia eccentrica [E ] “

Al posto della dizione angolo, in astronomia si usa “anomalia”. Come si vede dalla fig. 11b, l’anomalia media, Mø individuata da settore circolare zcy, si riferisce al moto di un satellite ideale che si muove in circolo con una velocità costante e con lo stesso periodo orbitale del satellite reale. L’anomalia media è dunque la distanza angolare dal centro della Terra fra il perigeo e il punto in cui si troverebbe il satellite nel suo moto medio in un particolare istante; il relativo punto y è tale che l’area del settore ellittico è uguale all’area del settore circolare zcy moltiplicato il rapporto tra i semiassi maggiore e minore, ossia zts=zcy*(bc/ac). La posizione reale del satellite e quindi l’anomalia vera v si applica al moto reale lungo un’orbita ellittica, mentre l’anomalia media si applica al moto medio del satellite ideale. Per individuare il punto x e quindi graficamente il punto y del satellite ideale con moto costante e la relativa posizione del satellite reale, viene utilizzata l’anomalia eccentrica E dove l’anomalia media è determinata dall’equazione di Keplero Mø = E – (e · sen E), poi l’anomalia vera viene messa in relazione a quella eccentrica con la seguente espressione (tutti gli angoli sono espressi in radianti):

tan(v/2)=(1+e/1-e)^0,5 · tan(E/2)

v =anomalia vera;
e =eccentricità;
E =anomalia eccentrica.

Nella comune pratica si usa considerare E=ma+∆ dove ∆ può essere ricavato dal normogramma di fig. 10. Con un righello si tracci una linea congiungendo la scala verticale a destra che visualizza i valori di ma, con la scala verticale a sinistra dove si leggono i valori di e. Il punto intercettato con la curva ci da il valore di ∆/e che moltiplicato per e ci da ∆. Al risultato va attribuito il segno mostrato sulla scala a destra.

Ad esempio, la linea che congiunge ma= 3,6 con e=0,6 intercetta la curva su ∆/e=0,3. Quindi si ha ∆=0,3 · 0,6 = 0,18. Il segno è negativo cosicché si ha: ∆ = – 0,18.

Quindi per mezzo dei dati dell’eccentricità e dell’anomalia media espressa in radianti, si deduce questo fattore di correzione; una volta ricavato E si applica l’equazione sopraddetta.
Per convertire da radianti in gradi moltiplicare per 180/π, per convertire da gradi in radianti moltiplicare per π/180
π=3,1415927

Fig.10 – Normogramma per il calcolo della anomalia eccentrica.

“La Phase”

Si è assunto con il termine phase i punti sull’orbita reale, determinati dall’equazione di Keplero, suddivisa in un numero stabilito di 256 punti di phase, posti a distanza variabile, come si vede dalla fig. 11a, in conformità con il moto reale (variabile) del satellite. Tale numero è stato scelto convenzionalmente in base alle combinazioni degli stati logici 0 e 1 in un sistema a 8 bit, infatti 256 corrisponde a 2⁸. Solo al perigeo e all’apogeo ma coincide con v dell’orbita ellittica e avranno rispettivamente un angolo di 360° (cui corrisponde una phase di 256) e 180° (cui corrisponde una phase di 128).

Fig. 11 – La phase e l’anomalia media.

“L’effetto giroscopico e l’asse Z del satellite”

Il satellite ha un asse di rotazione chiamato asse Z . AO10 per esempio compie circa 36 rpm sul proprio asse. I pannelli solari sono disposti in modo tale da produrre il massimo impiego della disponibilità della luce solare che deve essere perpendicolare all’asse Z. Questo asse determina anche il centro di riferimento della navetta spaziale nel quale procede il verso del fascio di radiazione di tutte le antenne, chiamato foro di visione del satellite. Ne consegue che i satelliti per telecomunicazioni devono poter mantenere un orientamento stabile in orbita. Il sistema di stabilizzazione più semplice ed economico utilizzato dai piccoli satelliti radioamatoriali, sfrutta l’effetto giroscopico, secondo il quale un corpo in rapida rotazione attorno ad uno dei suoi assi, tende a mantenere quest’asse allineato in una posizione fissa nello spazio. Quindi la simmetria assiale per questi satelliti è importante perché devono poter ruotare a grande velocità. Un meccanismo ausiliario deve poter imprime al satellite un rapido moto di rotazione da 500 a 1000 rivoluzioni per minuto (rpm) per avere la certezza di ottenere una perfetta stabilità al momento della sua separazione dal veicolo portante (shuttle o ultimo stadio del missile vettore).
Nonostante che un satellite non abbia punti cui riferire il proprio peso nel suo sistema inerziale, per il fatto che sfrutta questo effetto giroscopico, i suoi componenti elettronici devono essere assiemati in una idonea struttura poiché devono resistere alla forza centrifuga generata; ma una volta stabilizzato, un semplice dispositivo meccanico libera progressivamente e radialmente al proprio asse di rotazione dei cavi o bracci cui terminano dei pesi di pochi grammi; per effetto della conservazione del momento angolare, per una dimensione radiale più grande, la velocità viene ridotta drasticamente a pochi rpm.

Alon, Alat , Angolo di strabismo” [offpointing angle, offp]

L’alon e alat sono rispettivamente l’assetto longitudinale e latitudinale dell’asse Z del satellite. Per le loro definizioni vedi le fig. 12 a,b.

L’ angolo di strabismo è l’angolo formato dall‘asse Z del satellite con la retta di congiunzione del punto di osservazione della Terra con il satellite. Questo angolo è uguale a ø gradi quando l’asse Z cade sul punto di osservazione considerato. Conoscendo l’ampiezza angolare del fascio di radiazione dell’antenna del satellite, è possibile stimare di quanto si possa degradare il collegamento al variare di offp.

Esempio:
Se il satellite ha un’antenna con un’ampiezza del fascio a -3dB di 24 gradi, quando l’offp è di 12 gradi, significa che si sta subendo una perdita di -3 dB (metà della potenza).

Fig. 12 a/b – Angolo di strabismo.

“Effetto Doppler”

Le onde irradiate dall’antenna del satellite in fase di avvicinamento alla Terra, si comportano, per chi sta ricevendo, come se la loro lunghezza d’onda fosse più corta di quella originale, cosicché la frequenza di trasmissione del satellite risulta trovarsi più in alto di alcuni kHz rispetto quella effettivamente emessa; viceversa, quando il satellite si trova in fase di allontanamento, avviene il contrario, la frequenza di trasmissione del satellite risulta a terra trovarsi leggermente più in basso di quella originaria. Ciò accade come se le onde radio fossero le maglie di una molla che se viene compressa (fase di avvicinamento del satellite) si accorciano oppure se viene distesa (fase di allontanamento del satellite) si allungano.